Java에서 효율적인 경우의 수 따지기

C++의 next_permutation 구현

static boolean next_permutation(int[] a) {
        int i = a.length-1;
        while (i > 0 && a[i-1] >= a[i]) {
            i -= 1;
        }

        if (i <= 0) {
            return false;
        }

        int j = a.length-1;
        while (a[j] <= a[i-1]) {
            j -= 1;
        }

        int temp = a[i-1];
        a[i-1] = a[j];
        a[j] = temp;

        j = a.length-1;
        while (i < j) {
            temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i += 1;
            j -= 1;
        }
        return true;
    }

실사용 예시

경우의 수를 구하고 싶은 List의 숫자만큼 d[i] 로 Array를 구현한 다음, 해당 d[i] 를 next_permutation 돌린다.
do-while로 nextPermuation을 사용하는 모습. bitMask를 구현한 것과 같다

        int[] d = new int[store.size()];
        for (int i=0; i<m; i++) {
            d[i] = 1;
        }
        Arrays.sort(d);
        int ans = -1;
        do {
            int sum = 0;
            for (Pair p : people) {
                int min = -1;
                for (int i=0; i<store.size(); i++) {
                    if (d[i] == 0) continue;
                    Pair s = store.get(i);
                    int d1 = p.first-s.first;
                    int d2 = p.second-s.second;
                    if (d1 < 0) d1 = -d1;
                    if (d2 < 0) d2 = -d2;
                    int dist = d1+d2;
                    if (min == -1 || min > dist) {
                        min = dist;
                    }
                }
                sum += min; 
            }
            if (ans == -1 || ans > sum) {
                ans = sum;
            }
        } while (next_permutation(d));

---

순열 재귀함수 백트래킹으로 구현하기

제일 애용하는 방법. start index를 이용해서 경우의 수가 반복되지 않게 한방향으로 모든 순열의 경우를 구할 수 있다.

    static void go(int idx, String sum) {
        if (idx == n) {
            System.out.println(sum);
        }

        //전체 순열이라 매 숫자 Choice시에 전체 경우중 선택하지 않은 것 고려
        for(int i = 0; i < n; i++) {
            if(visited[i]) continue;
            //0으로 시작하는 숫자는 제외할 경우
            if(idx == 0 && A[i]== 0) continue;
            visited[i] = true;
            go( idx + 1, sum + A[i]);
            visited[i] = false;
        }
    }

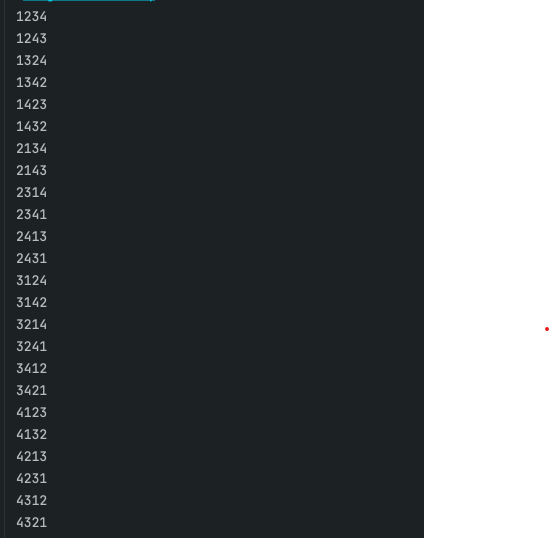
보통 모든 경우의 수 중에서 특정 조건을 충족하는 것들을 추출해낼 때 사용한다.

조합 재귀함수 백트래킹으로 구현하기

public class Main {
    static int[] A = {1,2,3,4};
    static boolean visited[] = new boolean[4];
    public static void main(String[] args) {
        go(0,0,"");
    }

    private static void go(int idx, int start, String sum) {
        if (idx == 3) {
            System.out.println(sum);
            return;
        }

        for (int i = start; i < 4; i++) {
            if (visited[i]) continue;
            visited[i] = true;
            go(idx + 1, i + 1, sum + A[i]); // 현재 인덱스 다음부터 시작
            visited[i] = false;
        }
    }
}

로또같은 것들은 49개의 숫자중에서 중복되지 않게 6개를 골라야 하는 경우다. 모든 로또의 경우는 순열이 아니라 조합이다.

---

bit로 경우의 수 구하기

모든 부분집합을 구할 때 편하다.

public class Main {
    static int[] A = {1,2,3,4};
    static boolean visited[] = new boolean[4];
    public static void main(String[] args) {

        for (int bit = 0; bit < (1 << 4); bit++) {//2의 4승으로 4가지 배열의 모든 on/off를 고려
            String sum = "";
            for (int i = 0; i < 4; i++) {//각 비트 자리수를 확인 ( ㅇ ㅇ ㅇ ㅇ )
                if ((bit & (1 << i)) != 0) {//i번째 비트가 1이면 i번째 원소 출력
                    sum += A[i];
                }
            }
            System.out.println(sum);

        }
    }
}

bit로 부분집합 구하기

public class Main {
    static int[] A = {1,2,3,4};
    static boolean visited[] = new boolean[4];
    public static void main(String[] args) {

        for (int bit = 0; bit < (1 << 4); bit++) {//2의 4승으로 4가지 배열의 모든 on/off를 고려
            String sum = "";
            int cnt = 0;
            for (int i = 0; i < 4; i++) {//각 비트 자리수를 확인 ( ㅇ ㅇ ㅇ ㅇ )
                if ((bit & (1 << i)) != 0) {//i번째 비트가 1이면 i번째 원소 출력
                    cnt++;
                    sum += A[i];
                }
            }

            if(cnt == 2) System.out.println(sum);

        }
    }
}

알고리즘의 최우선 고려대상은 브루트포스 (전체 탐색) 으로 가능한지, 아닌지이다. 지금까지 경우의 수를 구하는 다양한 방법을 알아봤는데 이 경우의 수 틀에서 문제에 맞게 사용하면 된다.

---

bit vs 재귀

비트 연산을 사용한 방법과 재귀를 사용한 방법은 각각의 상황에서 장단점이 있을 수 있다. 지금의 경우, 4개의 원소에서 2개를 선택하는 조합을 구하는 상황이므로 성능 차이는 거의 나지 않을 것이다.

• 1. 비트 연산:
     장점: 코드가 간결하고, 직관적입니다.
     단점: 문제의 규모가 커지면 비트 연산을 사용할 수 없는 경우가 발생할 수 있습니다. (32비트나 64비트 제한 등)
• 2. 재귀 호출:
     장점: 문제의 규모가 커져도 유연하게 대처할 수 있으며, 더 복잡한 문제에도 적용할 수 있습니다.
     단점: 코드가 조금 더 복잡하고, 재귀 호출에 따른 오버헤드가 있을 수 있습니다.
     그럼에도 불구하고, 위와 같은 작은 문제에서는 두 방법 모두 거의 동일한 성능을 보일 것입니다. 어떤 방식을 사용할지는 주로 코드의 가독성, 유지보수성, 확장성 등을 고려하여 결정하게 됩니다.

때에 따라서는 두 가지 방식을 혼합해서 사용하는 것도 좋은 방법이 될 수 있으니, 문제의 특성과 요구사항에 맞게 선택하면 된다.